power and torque curve, and maximum acceleration

[Murci.sv]

for the same gearbox ratio, at what moment is the acceleration felt (G force) the strongest? at maximum torque rpm or at maximum power rpm? and, when is the real acceleration of the vehicle the strongest?

[donkmeister]

Murci.sv said:

for the same gearbox ratio, at what moment is the acceleration felt (G force) the strongest? at maximum torque rpm or at maximum power rpm? and, when is the real acceleration of the vehicle the strongest?

Bit more complicated than that. Maximum power is when the greatest amount of kinetic energy per unit time is being added to the car, however as KE= 0.5 mv^2, the greatest amount of velocity being added per unit time could be lower down the revs, depending on the power Vs rpm graph.

Jerk is the rate of chance of acceleration; acceleration feels hardest when this rate of change is highest, which will be a transient such as reapplying drive after changing gear.

[GravelBen]

I *think* that on a simplified level it will be felt the most where the power curve is steepest, but the actual maximum acceleration will be at peak power.

But I could be wrong.

[mintmansam]

Murci.sv said:

for the same gearbox ratio, at what moment is the acceleration felt (G force) the strongest? at maximum torque rpm or at maximum power rpm? and, when is the real acceleration of the vehicle the strongest?

You will feel maximum G at maximum torque, if fixed in one gear with no clutch. You will obviously feel a greater G if you had a lower gear even if not at peak torque. It’s about wheel torque

Infact if you ignore air resistance (and other factors), you can actually plot G vs speed, per gear. Using the torque graph , gear ratios and mass of car

An example is these two cars below. G on Y axis and speed on X axis. Again a lot of theory here but you can see it’s basically the torque curve “squished” by the gear ratios

This shows why potentially an early gear change (normally only a few 100rpm) can be productive, on some cars with some gear ratios. But normally driving to redline is ideal way to keep maximum G. For reference this is two cars (blue and red) data



If you take 2nd gear on the blue can (second furthest left and second highest curve) you can see even though the engine torque and power can be at lowest point in rev range, nowhere in 3rd gear even at peak power or torque would the car out accelerate 2nd gear. This is the power of gear ratios.

Edited by mintmansam on Tuesday 12th December 00:50

Edited by mintmansam on Tuesday 12th December 00:56

[Murci.sv]

Jerk is the rate of chance of acceleration; acceleration feels hardest when this rate of change is highest, which will be a transient such as reapplying drive after changing gear.
[/quote].
ok, but how do you determine when the rate of change of acceleration is greatest? if the torque curve for example rises progressively constantly from 2000rpm up to 5500rpm (max peak) then remains more or less flat until 7000. at what point will the acceleration feel strongest.

in the m3 e46, the acceleration seemed to become stronger from 5000 then continued to pull until 8000. the torque decreased slightly from 5000-5500 however it did not seem so less strong

Edited by Murci.sv on Tuesday 12th December 00:55

[Murci.sv]

said:

this explains why the acceleration of m3 felt strongest around 5000-5500rpm

[Tye Green]

depends upon the external factors.

power to weight ratio theoretically determines the instantaneous acceleration but in practice friction and other stuff like wind resistance will increase with speed (thus consuming more of the available power) so the answer could be torque in certain applications!

[kambites]

For a particular gear, the point of maximum forward force asserting by the drive-train (assuming no wheel slip) will be at peak torque, however since the opposing forces increase with speed the maximum acceleration may come at a lower speed than that. It cannot come at a higher speed than peak torque (unless the car has some REALLY odd aerodynamics such that drag falls as speed rises).

Of course you'd accelerate even faster by changing down a gear to put you closer to peak power.

Edited by kambites on Tuesday 12th December 07:41

[kambites]

donkmeister said:

Murci.sv said:

Jerk is the rate of chance of acceleration; acceleration feels hardest when this rate of change is highest, which will be a transient such as reapplying drive after changing gear.

.
ok, but how do you determine when the rate of change of acceleration is greatest?

Jerk is the first derivative of acceleration (so the second derivative of speed) with respect to time. So the answer is calculous.

Or in simplistic terms, jerk is highest when the angle of the speed curve is steepest; which for a simple model with a fixed gear ratio and no wheel slip or drag, means the point where the torque curve is steepest.

Edited by kambites on Tuesday 12th December 07:44

[GT9]

Accelerative force is determined by the torque of the engine multiplied by the gear ratio.
The highest accelerative force will therefore be felt in first gear at peak torque, assuming loss of traction doesn't come into it.
For high-powered two wheel drive cars, that is often the case though.
In terms of the ever-present forces slowing the car down, drag force increases with the square of speed, rolling resistance is quasi-fixed.
Higher gears (i.e. a lower overall ration between the engine and the driven wheels) won't only have less torque at the wheels, they also have more drag force to overcome, so the accelerative force will be substantially less than it is in first gear unless loss of traction occurs.
The power to overcome drag increases with the cube of speed, and the power to overcome rolling resistance increases linearly with speed.
The power to add kinetic energy at fixed rate of acceleration increases linearly with speed and can be calculated with this rule of thumb: 6 bhp per ton per g per mph.
All of which is why big power is needed for very high speeds.
Maximum power in first gear more often than not goes to waste as the car can't deploy it.

[braddo]

kambites said:

Jerk is the first derivative of acceleration (so the second derivative of speed) with respect to time. So the answer is calculous.

Or in simplistic terms, jerk is highest when the angle of the speed curve is steepest; which for a simple model with a fixed gear ratio and no wheel slip or drag, means the point where the torque curve is steepest.

Wouldn't 'jerk' be the greatest where the power curve is steepest (not torque)? I don't think high revving NA stuff has peak jerk where the torque curve is steepest. Honda S2000, 911 GT3s, Toyota Elises etc.

[Murci.sv]

kambites said:

donkmeister said:

Murci.sv said:

Jerk is the rate of chance of acceleration; acceleration feels hardest when this rate of change is highest, which will be a transient such as reapplying drive after changing gear.

.
ok, but how do you determine when the rate of change of acceleration is greatest?

Jerk is the first derivative of acceleration (so the second derivative of speed) with respect to time. So the answer is calculous.

Or in simplistic terms, jerk is highest when the angle of the speed curve is steepest; which for a simple model with a fixed gear ratio and no wheel slip or drag, means the point where the torque curve is steepest.

Edited by kambites on Tuesday 12th December 07:44

this explains why a lot of turbos feel super fast or even scary for single turbos with stiff power and very high jerk. while sometimes very powerful NAs feel rather manageable and slower.

[Crudeoink]

Id have thought it wouldnt matter how steep the torque curve was, if you had a flat curve from 500rpm-5000rpm you'd still accelerate, because the rate of torque delivery is increasing amd torque is staying constant. But I dont think torque really matters here. Surely it would be where the delta between engine power and resistive forces (rolling & air) are at their highest.

To explain why the torque doesnt matter, an engine making 1000nm at 50 rpm = 7hp
And engine making 300nm at 7500rpm is making 316hp

[tapkaJohnD]

I've only heard of "jerk", the second derivative of velocity, in the design of roller-coasters, where the third derivative is "jolt"

[trevalvole]

braddo said:

Wouldn't 'jerk' be the greatest where the power curve is steepest (not torque)? I don't think high revving NA stuff has peak jerk where the torque curve is steepest. Honda S2000, 911 GT3s, Toyota Elises etc.

I think, having not done this kind of thing for sometime, that peak torque occurs at the point of maximum rate of change of power:

Power = Torque x Omega (which is angular velocity)

differentiate this with respect to Omega:

Rate of change of Power with angular velocity = Torque

On a less mathematical level, this makes sense to me as at peak acceleration in a gear (which is at peak torque ignoring aerodynamics and friction etc: alpha (which is angular acceleration) = Torque/Inertia), it is at the point that the greatest increase of power/energy is going into the mass of the car, as with increasing speed the car will have higher kinetic energy.

[ATG]

kambites said:

It cannot come at a higher speed than peak torque (unless the car has some REALLY odd aerodynamics such that drag falls as speed rises).

Mental picture of TVR shedding bodywork as speed increases

[GT9]

Crudeoink said:

Id have thought it wouldnt matter how steep the torque curve was, if you had a flat curve from 500rpm-5000rpm you'd still accelerate, because the rate of torque delivery is increasing amd torque is staying constant. But I dont think torque really matters here. Surely it would be where the delta between engine power and resistive forces (rolling & air) are at their highest.

To explain why the torque doesnt matter, an engine making 1000nm at 50 rpm = 7hp
And engine making 300nm at 7500rpm is making 316hp

Torque is force, it matters.
Torque is a measure of how capable the car is to increase speed from the current speed.
Power is needed as the speed climbs.
By far the largest consumer of power at sub 100 mph is power required to accelerate.
Ias already posted this is a fixed equation of 6 bhp per ton per mph per g.
Accelerating at 1 g from 10 mph ONLY requires 60 bhp per ton.
At 100 mph it requires 600 bhp per ton.

[Crudeoink]

GT9 said:

Torque is force, it matters.
Torque is a measure of how capable the car is to increase speed from the current speed.
Power is needed as the speed climbs.
By far the largest consumer of power at sub 100 mph is power required to accelerate.
Ias already posted this is a fixed equation of 6 bhp per ton per mph per g.
Accelerating at 1 g from 10 mph ONLY requires 60 bhp per ton.
At 100 mph it requires 600 bhp per ton.

If torque were a measure of how capable a car is to increase speed why are race cars and bikes short stroke high revving engines? 10,000nm at 1rpm isnt going to get you anywhere very quick.

As for part 2 about the weight, it can be ignored for now, the question wasn't is a lighter car faster, it was asking if acceleration is higher at max torque or max revs. (so assuming the same car but assessing 2 different parts of the rev range)

The maximum speed of a vehicle is determined by the balance of forces acting on it, primarily the power generated by its engine and the resistance forces it encounters. These resistance forces include air resistance, rolling resistance, and the force due to gravity on a slope. The exact equation for calculating top speed will vary depending on the specific vehicle and driving conditions, but a general approach can be outlined using the following steps:

Determine the engine power (P): This is the maximum power output of the vehicle's engine , measured in horsepower or kilowatts.

Calculate the power required to overcome aerodynamic drag (Pd): Aerodynamic drag increases with speed, and it can be approximated by the following equation:

Pd = 0.5ρACdv²

where:

ρ = Density of air (approximately 1.2 kg/m³ at standard sea level)
A = Vehicle cross-sectional area perpendicular to airflow
Cd = Aerodynamic drag coefficient, which is dependent on the vehicle's shape and design
v = Vehicle speed

Calculate the power required to overcome rolling resistance (Pr): Rolling resistance is a constant force that opposes the movement of a vehicle, and it can be approximated by the following equation:

Pr = μmg

where:

μ = Rolling resistance coefficient, typically between 0.005 and 0.01 for modern vehicles
m = Vehicle mass (in kg)
g = Acceleration due to gravity (approximately 9.81 m/s²)

Calculate the power required to overcome slope resistance (Ps): If the vehicle is traveling uphill on a slope, it will encounter an additional resistance force due to gravity. This force can be calculated by:

Ps = mgsinθ

where:

θ = Angle of the slope (in degrees)

Determine the total power required to maintain constant speed (Ptotal): This is the sum of the powers required to overcome aerodynamic drag, rolling resistance, and slope resistance.

Ptotal = Pd + Pr + Ps

Set the total power equal to the engine power (Ptotal = P): This gives an equation for the maximum speed of the vehicle:

v = √((Ptotal/P) / (0.5ρAC))

Given this I would say maximum acceleration would occur at the Rpm where the difference between engine power and resistance(s) on the vehicle is at its greatest.

• Editted some typo's i had missed

Edited by Crudeoink on Tuesday 12th December 13:43

[Pica-Pica]

tapkaJohnD said:

I've only heard of "jerk", the second derivative of velocity, in the design of roller-coasters, where the third derivative is "jolt"

Back to origins.
The first derivative of position is velocity.
The second derivative of position is acceleration.
The third derivative of positions is jerk.
The fourth derivative of position is snap.
In theory there are more derivatives (and, they have been named by some as crackle and pop)

[GT9]

Crudeoink said:

GT9 said:

Torque is force, it matters.
Torque is a measure of how capable the car is to increase speed from the current speed.
Power is needed as the speed climbs.
By far the largest consumer of power at sub 100 mph is power required to accelerate.
Ias already posted this is a fixed equation of 6 bhp per ton per mph per g.
Accelerating at 1 g from 10 mph ONLY requires 60 bhp per ton.
At 100 mph it requires 600 bhp per ton.

If torque were a measure of how capable a car is to increase speed why are race cars and bikes short stroke high revving engines? 10,000nm at 1rpm isnt going to get you anywhere very quick.

As for part 2 about the weight, it can be ignored for now, the question wasn't is a lighter car faster, it was asking if acceleration is higher at max torque or max revs. (so assuming the same car but assessing 2 different parts of the rev range)

The maximum speed of a vehicle is determined by the balance of forces acting on it, primarily the power generated by its engine and the resistance forces it encounters. These resistance forces include air resistance, rolling resistance, and the force due to gravity on a slope. The exact equation for calculating top speed will vary depending on the specific vehicle and driving conditions, but a general approach can be outlined using the following steps:

Determine the engine power (P): This is the maximum power output of the vehicle's engine , measured in horsepower or kilowatts.

Calculate the power required to overcome aerodynamic drag (Pd): Aerodynamic drag increases with speed, and it can be approximated by the following equation:

Pd = 0.5?ACdv²

where:

? = Density of air (approximately 1.2 kg/m³ at standard sea level)
A = Vehicle cross-sectional area perpendicular to airflow
Cd = Aerodynamic drag coefficient, which is dependent on the vehicle's shape and design
v = Vehicle speed

Calculate the power required to overcome rolling resistance (Pr): Rolling resistance is a constant force that opposes the movement of a vehicle, and it can be approximated by the following equation:

Pr = ?mg

where:

? = Rolling resistance coefficient, typically between 0.005 and 0.01 for modern vehicles
m = Vehicle mass (in kg)
g = Acceleration due to gravity (approximately 9.81 m/s²)

Calculate the power required to overcome slope resistance (Ps): If the vehicle is traveling uphill on a slope, it will encounter an additional resistance force due to gravity. This force can be calculated by:

Ps = mgsin?

where:

? = Angle of the slope (in degrees)

Determine the total power required to maintain constant speed (Ptotal): This is the sum of the powers required to overcome aerodynamic drag, rolling resistance, and slope resistance.

Ptotal = Pd + Pr + Ps

Set the total power equal to the engine power (Ptotal = P): This gives an equation for the maximum speed of the vehicle:

v = ?((Ptotal/P) / (0.5?AC))

Given this I would say maximum acceleration would occur at the Rpm where the difference between engine power and resistance(s) on the vehicle is at its greatest.

• Editted some typo's i had missed

Edited by Crudeoink on Tuesday 12th December 13:43

You are conflating force as being 'the same as' power, it very much is not.
You need to go back to engineering first principles.

Power = force x velocity

What that means is that is the power required depends on what speed you are travelling at, generally, the force does not.
The only force acting on the car that has a speed dependency is drag force.
The force to accelerate the car at a given rate of acceleration is independent of speed, as is the force to overcome rolling resistance.

All of the torque values you have been referring to are at the engine, NOT at the wheels.
The multi-ratio gearboxes on ICE engine vehicles confuse the understanding of the fundamental principles of motion for two reasons.

Firstly, because they give access to the engine's full power output at low road speed, which is totally unnecessary, it's simply a function of having high ratios between the engine and the driven wheels to provide sufficient acceleration at low speed from an imperfect torque device, i.e. an engine. By imperfect, I mean that the engine cannot produce the same torque at all rpm.

Secondly, the torque figure that manufacturers and everyone quotes are the torque at the engine output. The gearbox then multiplies that torque by different amount, depending on what gear you are in.
The same torque in first gear provides a higher accelerative force than it will in second gear, but the engine runs out of revs to go any faster, so second gear must be selected.
Nobody, except me it seems, has every quoted or referred to driven wheel torques, yet that's the actual torque turning the driven wheels and providing the acceleration.
It's easier to understand all of this by taking the multi-ratio gearbox out of the equation, as is the case with a single speed powertrain, such as that in an EV.
The EV also has a perfect torque device driving it, i.e. an electric motor that can provide the same torque at all rpms.
I concede that statement is not entirely true, because most EVs have a motor that operates in two regimes, fixed torque (up to say 60 mph) and the fixed power (over 60 mph). The reason for this is related to engineering optimisation to do with battery voltages, and typical drive cycles, amongst other thing , so rather than confuse the issue, let's just examine the fixed torque regime.

Here is a plot for a typical large EV.
It shows the individual power demands required to overcome drag, rolling resistance and the power required to accelerate the car at different g values. The acceleration power needs to be read of the righthand vertical axis, the permanent consumers of the left hand vertical axis.



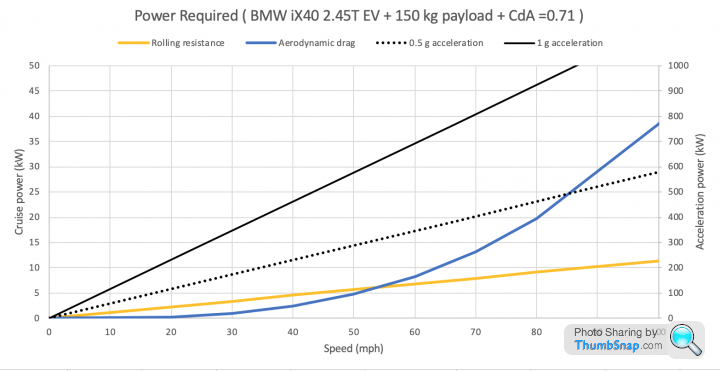
None of the power demands are high at low road speeds, they all start from zero.
It is totally unnecessary to have high power output at low road speed.
Here is proof, this is the power output plot of one of the fastest accelerating production cars ever, one that is also a very heavy car by most measures. It also has no multi-ratio gearbox.



The reason it can accelerate so quickly to 60 mph is because it is supplying a fixed value of driven wheel torque at all road speeds up to 60 mph. This results in the power output rising linearly from zero to full power over the 0-60 run.

The torque at the driven wheels is what is providing the ability for the speed to increase, the power is simply a measure of how fast you are travelling.

Torque matters, it is what is providing the instantaneous force.

Power and the resulting energy consumption that is defined by power multiplied by time, is essentially a measure of how long this force can be sustained for, either to keep the car moving or to accelerate it.

To accelerate, the car must be able to increase the instantaneous torque at the driven wheels, otherwise nothing will happen.

If you want to understand the role the gearbox plays, here is a plot showing the comparison between two similar cars, a Golf GTI and a Cupra Born. Despite the fact that the EV cannot muster full power until 60 mph, it accelerates at the around same rate as the Golf which gives access to full power at 30 mph. Look at the driven wheel torque curves for the two cars. The ICE drivetrain is trying to mimic the fixed driven wheel torque of the EV, and it does so by supplying excessive torque to make up for the sections where it has less torque. The gear change in the Golf is at 35 mph.



The data supplied above for the BMW, the Golf and the Cupra is my own, obviously the Tesla plot comes straight from their website.

Note that EVs do have a fixed final drive ratio between the motor and the wheels, so even the quoted torque values for these you always read about, e.g. 350 Nm only tell you what the motor is producing, they DO NOT tell you what is being supple to the driven wheels.
You can only determine this if you know the final drive ratio, in the case of the Born, its about 8:1, which is why the driven wheel torque is just over 3000 Nm.
A small number of EVs also have second gear ratio to optimise high speed driving, the Taycan for example.

And finally, just to complicate things a bit more, converting driven wheel torque into the actual accelerative force or force to overcome drag/friction depends on the working outer radius of the tyres, which can alter slightly with speed/wear, as well as obviously differing between cars.

All of which is why people try to define acceleration by power-to-weight ratios, as it takes the engine's instantaneous torque value, the gearing being used at a given speed and tyre diameters out of the discussion.

The key thing to remember though is that the power required to accelerate is not a fixed value, it depends entirely on speed.

Hence the rule of thumb I posted at the beginning of the thread:

6 bhp per ton per g per mph.

Edited by GT9 on Tuesday 12th December 17:11