Maths help please...
Discussion
I'm embarrassed to say my school boy maths is letting me down. Where once I could competently apply Maxwell's equations now I can't calculate a basic school boy maths problem :-(
Can you help?
The problem: My driveway is made of concrete, long, sloping and uneven. It has a particularly large dip that causes all cars going up it to go on 3 wheels and any van or concrete mixer etc to tilt at a perilous angle that frightens the life out of the driver. It's time to fill the dip to level it off. My problem is calculating how much concrete volume I need.
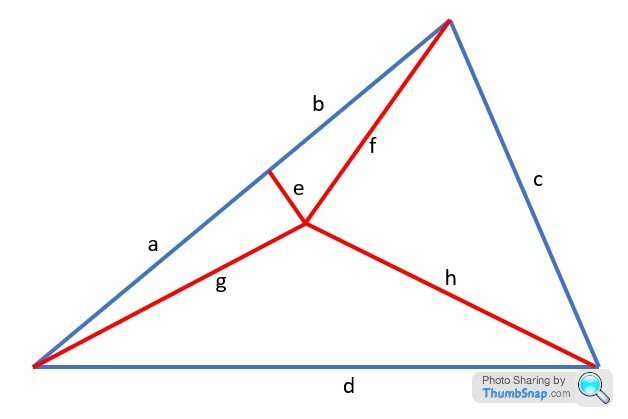
Below is a diagram of the dip:
1 - The blue lines are as viewed from above and give the surface area that needs concrete applying to it.
2 - The red lines converge at the deepest point of the dip.
3 - Line "e" is at right angles to ab and h and is effectively at the side of the driveway. So at the moment as you drive up the driveway your left hand wheels follow the line g-f whereas your right hand wheels follow a nice straight line hence the perilous tilt to the left that causes vehicles to go up on 3 wheels.
In terms of a,b,c,d,e,f,g,h how much concrete volume do I need?
I thought it would be really easy to simply calculate it as: volume = a*e*h/4 + b*e*h/4 but now I am not so sure. Am I right or wrong?
ETA: ETA - Sorry I realise now that is not clear. Line e is vertical at the edge of the driveway. abgf are a vertical surface at the side of the driveway. So e is in effect the height or depth.
Many thanks.
Can you help?
The problem: My driveway is made of concrete, long, sloping and uneven. It has a particularly large dip that causes all cars going up it to go on 3 wheels and any van or concrete mixer etc to tilt at a perilous angle that frightens the life out of the driver. It's time to fill the dip to level it off. My problem is calculating how much concrete volume I need.
Below is a diagram of the dip:
1 - The blue lines are as viewed from above and give the surface area that needs concrete applying to it.
2 - The red lines converge at the deepest point of the dip.
3 - Line "e" is at right angles to ab and h and is effectively at the side of the driveway. So at the moment as you drive up the driveway your left hand wheels follow the line g-f whereas your right hand wheels follow a nice straight line hence the perilous tilt to the left that causes vehicles to go up on 3 wheels.
In terms of a,b,c,d,e,f,g,h how much concrete volume do I need?
I thought it would be really easy to simply calculate it as: volume = a*e*h/4 + b*e*h/4 but now I am not so sure. Am I right or wrong?
ETA: ETA - Sorry I realise now that is not clear. Line e is vertical at the edge of the driveway. abgf are a vertical surface at the side of the driveway. So e is in effect the height or depth.
Many thanks.

Edited by anonymous-user on Saturday 20th March 16:53
Ignore line e for the time being. You have a cavity that is an inverted triangle-based pyramid (aka an irregular tetrahedron). The base of the pyramid is (a+b), c and d, and the edges that met at the apex are f, g and h.
You have to know how tall the pyramid is to know the required volume - in other words how much lower the meeting point of e, f, g and h is than the plane of the lines a+b, c and d.
See here for how to work out the volume of an irregular tetrahedron: http://mathcentral.uregina.ca/QQ/database/QQ.09.03...
You have to know how tall the pyramid is to know the required volume - in other words how much lower the meeting point of e, f, g and h is than the plane of the lines a+b, c and d.
See here for how to work out the volume of an irregular tetrahedron: http://mathcentral.uregina.ca/QQ/database/QQ.09.03...
Think you’re missing a bit of information there. The volume of any irregular tetrahedron is:
1/3 x height x area of base
Assuming the line a+b is straight, then the area of the base is is simply the area of the triangle (a+b)/c/d which can be calculated using Heron’s formula.
But you’re missing the height (or in your case, depth). If you’ve got that then you can calculate the volume.
Tip: to find depth, fill the area with water and measure the depth to surface at deepest point. In fact, could use litres of water needed to fill it to work out volume...
1/3 x height x area of base
Assuming the line a+b is straight, then the area of the base is is simply the area of the triangle (a+b)/c/d which can be calculated using Heron’s formula.
But you’re missing the height (or in your case, depth). If you’ve got that then you can calculate the volume.
Tip: to find depth, fill the area with water and measure the depth to surface at deepest point. In fact, could use litres of water needed to fill it to work out volume...
67Dino said:
Think you’re missing a bit of information there. The volume of any irregular tetrahedron is:
1/3 x height x area of base
Assuming the line a+b is straight, then the area of the base is is simply the area of the triangle (a+b)/c/d which can be calculated using Heron’s formula.
But you’re missing the height (or in your case, depth). If you’ve got that then you can calculate the volume.
Tip: to find depth, fill the area with water and measure the depth to surface at deepest point. In fact, could use litres of water needed to fill it to work out volume...
Hi. ab is strtaight. The depth (as you say :-) ) is e1/3 x height x area of base
Assuming the line a+b is straight, then the area of the base is is simply the area of the triangle (a+b)/c/d which can be calculated using Heron’s formula.
But you’re missing the height (or in your case, depth). If you’ve got that then you can calculate the volume.
Tip: to find depth, fill the area with water and measure the depth to surface at deepest point. In fact, could use litres of water needed to fill it to work out volume...
e is at right angles to ab and h.
ETA - Sorry I realise now that is not clear. Line e is vertical at the edge of the driveway. abgf are a vertical surface at the side of the driveway. So e is in effect the height or depth.
Edited by anonymous-user on Saturday 20th March 16:52
BlackTails said:
Ignore line e for the time being. You have a cavity that is an inverted triangle-based pyramid (aka an irregular tetrahedron). The base of the pyramid is (a+b), c and d, and the edges that met at the apex are f, g and h.
You have to know how tall the pyramid is to know the required volume - in other words how much lower the meeting point of e, f, g and h is than the plane of the lines a+b, c and d.
See here for how to work out the volume of an irregular tetrahedron: http://mathcentral.uregina.ca/QQ/database/QQ.09.03...
Hi sorry I was not clear. Line e is vertical at the edge of the driveway. abgf are a vertical surface at the side of the driveway. So e is in effect the height or depth.You have to know how tall the pyramid is to know the required volume - in other words how much lower the meeting point of e, f, g and h is than the plane of the lines a+b, c and d.
See here for how to work out the volume of an irregular tetrahedron: http://mathcentral.uregina.ca/QQ/database/QQ.09.03...
This doesn't actually address your maths question, but I'm wondering if it's a viable alternative to line the sunken area carefully with plastic sheet, and then fill it with water from some kind of container which holds a known volume of water, to see how much water is used to fill the hole? That should give you the volume.
i.e. do the opposite of Archimedes's "Eureka" moment in the bathtub?
EDIT: I see this has already been suggested. oops!
i.e. do the opposite of Archimedes's "Eureka" moment in the bathtub?
EDIT: I see this has already been suggested. oops!
Edited by kiseca on Tuesday 23 March 13:21
If the link by BlackTails doesn't fit the bill, you might find this is helpful. It allows you to find the volume of a "triangular" pyramid, which if I understand your diagram, you could add a series of these together to get a decent approximation.
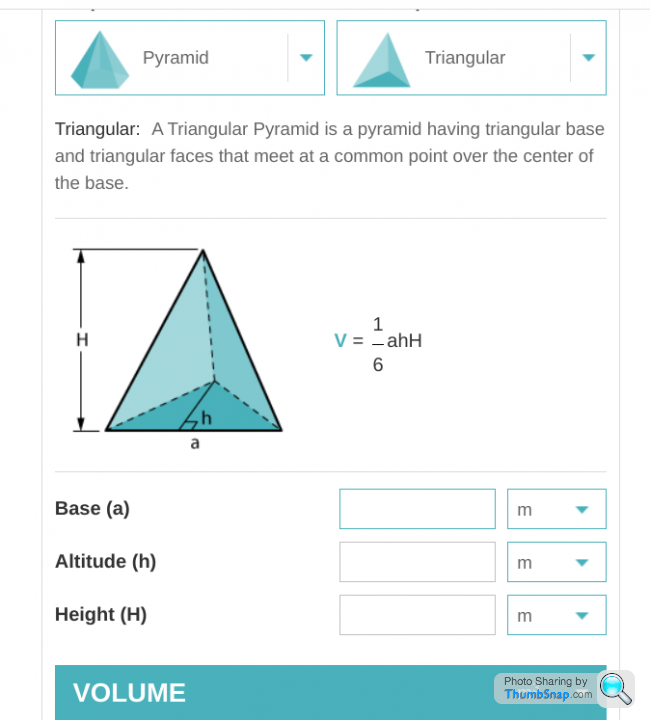
https://www.trelleborg.com/en/seals/Resources/Desi...

https://www.trelleborg.com/en/seals/Resources/Desi...
EddieSteadyGo said:
If the link by BlackTails doesn't fit the bill, you might find this is helpful. It allows you to find the volume of a "triangular" pyramid, which if I understand your diagram, you could add a series of these together to get a decent approximation.

https://www.trelleborg.com/en/seals/Resources/Desi...
Thanks. Aiming to take some measurements at the weekend then jetwash the area etc and order in a few weeks time before the weather gets too hot. I'll look more closely at yours and BlackTails links then.
https://www.trelleborg.com/en/seals/Resources/Desi...
The issue I have is I'd rather have too much concrete than not enough.... but whilst I can dispose of a small amount of extra I can't be doing with having half a cubic metre too much! That said I could fill the potholes within a 200Metre radius if I did have surplus!
EddieSteadyGo said:
If the link by BlackTails doesn't fit the bill, you might find this is helpful. It allows you to find the volume of a "triangular" pyramid, which if I understand your diagram, you could add a series of these together to get a decent approximation.

https://www.trelleborg.com/en/seals/Resources/Desi...
Split the volume into two inverted pyramids by joining the top of line e with the intersection of c d then use the online calculator to determine the volume of the two pyramids then add the two volumes together. 
https://www.trelleborg.com/en/seals/Resources/Desi...
The lines a+b, c and d define a plane. If that plane is horizontal, you could as other have suggested fill the hole with water, measure the volume of water and use that to work out your concrete requirements.
But if that plane isn’t horizontal, then you won’t be able to fill the hole fully: if say the apex where c and d meet is lower than the line a+b, water will overflow at that apex before the surface level gets to the level of a+b.
While concrete is more viscous than water, you’re liable to suffer the same issue on a lesser scale if you pour concrete into the hole. Do you need to build up edges c and d to create a horizontal plane bounded by a+b, c and d?
But if that plane isn’t horizontal, then you won’t be able to fill the hole fully: if say the apex where c and d meet is lower than the line a+b, water will overflow at that apex before the surface level gets to the level of a+b.
While concrete is more viscous than water, you’re liable to suffer the same issue on a lesser scale if you pour concrete into the hole. Do you need to build up edges c and d to create a horizontal plane bounded by a+b, c and d?
BlackTails said:
The lines a+b, c and d define a plane. If that plane is horizontal, you could as other have suggested fill the hole with water, measure the volume of water and use that to work out your concrete requirements.
But if that plane isn’t horizontal, then you won’t be able to fill the hole fully: if say the apex where c and d meet is lower than the line a+b, water will overflow at that apex before the surface level gets to the level of a+b.
While concrete is more viscous than water, you’re liable to suffer the same issue on a lesser scale if you pour concrete into the hole. Do you need to build up edges c and d to create a horizontal plane bounded by a+b, c and d?
Just add some fibre to the mixBut if that plane isn’t horizontal, then you won’t be able to fill the hole fully: if say the apex where c and d meet is lower than the line a+b, water will overflow at that apex before the surface level gets to the level of a+b.
While concrete is more viscous than water, you’re liable to suffer the same issue on a lesser scale if you pour concrete into the hole. Do you need to build up edges c and d to create a horizontal plane bounded by a+b, c and d?
Gassing Station | Science! | Top of Page | What's New | My Stuff



