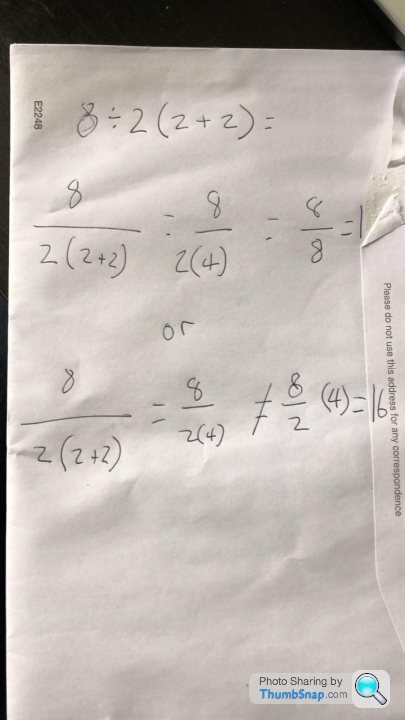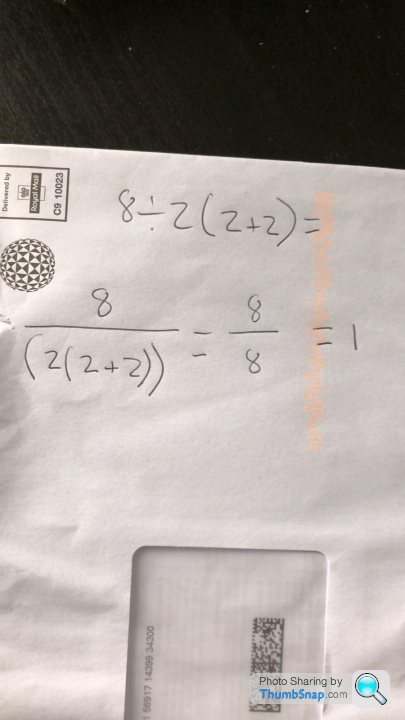Maths question, apparently gone viral ion 2019
Discussion
https://twitter.com/pjmdolI/status/115559805095974...
Quite amusing posts. You're wrong and I am right ... etc etc.
Quite amusing posts. You're wrong and I am right ... etc etc.
I'm not sure this is the right way to solve this equation and happy for somebody to point out the error of my ways, but I sometimes like to give a real world scenario to these and see what the result is. 8 Footballers run out on to the pitch and divide themselves in 1/2 so they can have a 4 vs 4 match. They are each wearing 2 football boots and 2 gloves, how many gloves and football boots are there in total?
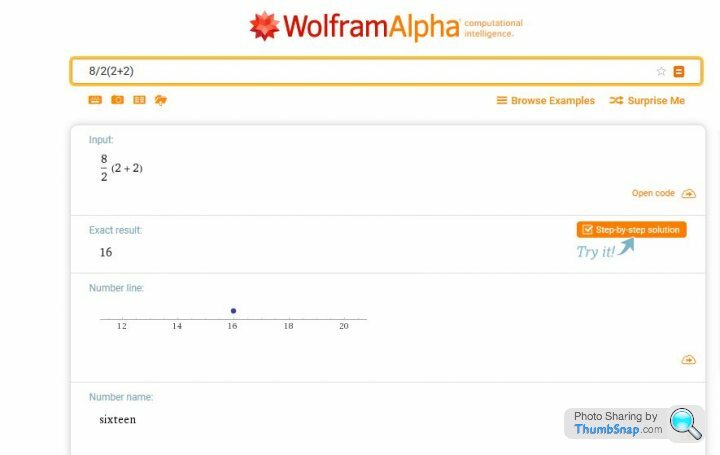
8/2(2+2) = well in the scenario above it'd be 16.
8/2(2+2) = well in the scenario above it'd be 16.
MECHENG84 said:
I'm not sure this is the right way to solve this equation and happy for somebody to point out the error of my ways, but I sometimes like to give a real world scenario to these and see what the result is. 8 Footballers run out on to the pitch and divide themselves in 1/2 so they can have a 4 vs 4 match. They are each wearing 2 football boots and 2 gloves, how many gloves and football boots are there in total?
8/2(2+2) = well in the scenario above it'd be 16.
You are both the giver of a good example and more importantly correct.8/2(2+2) = well in the scenario above it'd be 16.
Problem is, priority isn't 100% defined 
Using my Casio FX85GT Plus;
8/2(2+2) =1 - the implied multiplication has priority
8/2x(2+2) =16 - specifying the multiply changes the priority!
and my FX85ES gives 16 for both inputs
The nice thing about standards is there are so many to choose from

Using my Casio FX85GT Plus;
8/2(2+2) =1 - the implied multiplication has priority
8/2x(2+2) =16 - specifying the multiply changes the priority!
and my FX85ES gives 16 for both inputs

The nice thing about standards is there are so many to choose from
Gojira said:
Problem is, priority isn't 100% defined 
Using my Casio FX85GT Plus;
8/2(2+2) =1 - the implied multiplication has priority
8/2x(2+2) =16 - specifying the multiply changes the priority!
and my FX85ES gives 16 for both inputs
The nice thing about standards is there are so many to choose from
Id have gone with the first as the "2(4)" indicates you still need to solve the brackets to me...
Using my Casio FX85GT Plus;
8/2(2+2) =1 - the implied multiplication has priority
8/2x(2+2) =16 - specifying the multiply changes the priority!
and my FX85ES gives 16 for both inputs

The nice thing about standards is there are so many to choose from
I always figured with BODMAS, to "solve" the brackets they had to be removed from the equation and that only happens when you sort the multiplication out first :P
Jakeztx said:
Gojira said:
Problem is, priority isn't 100% defined 
Using my Casio FX85GT Plus;
8/2(2+2) =1 - the implied multiplication has priority
8/2x(2+2) =16 - specifying the multiply changes the priority!
and my FX85ES gives 16 for both inputs
The nice thing about standards is there are so many to choose from
Id have gone with the first as the "2(4)" indicates you still need to solve the brackets to me...
Using my Casio FX85GT Plus;
8/2(2+2) =1 - the implied multiplication has priority
8/2x(2+2) =16 - specifying the multiply changes the priority!
and my FX85ES gives 16 for both inputs

The nice thing about standards is there are so many to choose from
I always figured with BODMAS, to "solve" the brackets they had to be removed from the equation and that only happens when you sort the multiplication out first :P

Back when the world was young, and I did A-level maffs, I was taught that solving the brackets consisted of replacing them with the single number result, so I'd have gone with 16 as an answer, but I've been up the pub since then, so I'm not as sure as I'd like to be - especially when Wikipedia doesn't help

Mr Pointy said:
Scabutz said:
Mr Pointy said:
BODMAS, it's always BODMAS.
Apparently not when its PEMDAS, whatever that is. I was always taught BODMAS. Now my kids tell me its BIDMASScabutz said:
Mr Pointy said:
Scabutz said:
Mr Pointy said:
BODMAS, it's always BODMAS.
Apparently not when its PEMDAS, whatever that is. I was always taught BODMAS. Now my kids tell me its BIDMAS8/2(2+2)
= 8/2(4)
= 8/8 <---- Brackets fully resolved
= 1
Scabutz said:
Mr Pointy said:
Scabutz said:
Mr Pointy said:
BODMAS, it's always BODMAS.
Apparently not when its PEMDAS, whatever that is. I was always taught BODMAS. Now my kids tell me its BIDMASotolith said:
This has been going on for ages. It's a classic clickbait trick, pick something that people will argue about. That division operator is the problem - it's poorly defined. Grown-ups doing mathematics don't use it, it's for children doing arithmetic.
That's wrong actually.Wrong in that it's the division symbol used that it is just clickbait. Instead think of it as a way to correct your maths assumptions. You are correct that it is an old issue and it is poorly defined.
OK, the solution is that it can be either 1 or 16 using mathematical rules due to the equation being badly written so being ambiguous.
Note that PEDMAS or PEMDAS or BODMAS or BIDMAS is not a mathematical rule, it's a mnemonic and prone to misinterpretation. So it is no wonder people are getting that wrong.
The reasoning for 1 and 16 both being correct --
The equation of 8÷2(2×2) = ? can obviously be reduced first without any argument to
8÷2(4) = ?
and then again
8÷2×4 = ? or 8 / 2 × 4 = ?
This where the problem starts and it is not the maths rules but how people have learnt how to do it. People may grasp at
1. It is always division first.
2. It is done left to right.
Both are wrong. M and D do not have priority in maths, neither are they done left to right, unlike Add and Subtraction which is. PEDMAS or PEMDAS or BODMAS etc is not a maths rule. It's a memory aid which is being used wrongly.
With 8÷2×4 or 8 / 2 × 4 there is not enough information as written to decide which operation to do first as no priority. If you choose one way you get one answer, the other way the 2nd answer.
The equation is badly written. It can be better written on 2 lines using / or on one line using parentheses, ie
8÷(2×4) or (8÷2)×4
8
-------
2 × 4
or
8 × 4
---
2
No doubt it will pop up again in a few years time using different numbers ( to protect the innocent )
PS Note that PEDMAS is better written P -- E -- DM ( MD) -- AS (SA) left to right
if you wish to use it
Note that PEDMAS or PEMDAS or BODMAS or BIDMAS is not a mathematical rule, it's a mnemonic and prone to misinterpretation. So it is no wonder people are getting that wrong.
The reasoning for 1 and 16 both being correct --
The equation of 8÷2(2×2) = ? can obviously be reduced first without any argument to
8÷2(4) = ?
and then again
8÷2×4 = ? or 8 / 2 × 4 = ?
This where the problem starts and it is not the maths rules but how people have learnt how to do it. People may grasp at
1. It is always division first.
2. It is done left to right.
Both are wrong. M and D do not have priority in maths, neither are they done left to right, unlike Add and Subtraction which is. PEDMAS or PEMDAS or BODMAS etc is not a maths rule. It's a memory aid which is being used wrongly.
With 8÷2×4 or 8 / 2 × 4 there is not enough information as written to decide which operation to do first as no priority. If you choose one way you get one answer, the other way the 2nd answer.
The equation is badly written. It can be better written on 2 lines using / or on one line using parentheses, ie
8÷(2×4) or (8÷2)×4
8
-------
2 × 4
or
8 × 4
---
2
No doubt it will pop up again in a few years time using different numbers ( to protect the innocent )
PS Note that PEDMAS is better written P -- E -- DM ( MD) -- AS (SA) left to right
if you wish to use it
Edited by Gandahar on Friday 2nd August 15:01
Gassing Station | Science! | Top of Page | What's New | My Stuff