Snells Law, relative refractive indices!

[vinnie83]

Hello science people, I need some help!

I am a mature student and as part of the current course I am doing, I have a physics exam on Monday.

I am slightly confused about the aforementioned subject, and googling seems to confuse me more so I was hoping for someone who may be able to spare a few moments to help:





Now the 2nd image is from when I took notes in class, and it made perfect sense at the time....

I follow the maths all the way down to the Sin-1 - I get that we are moving the Sin to the other side of the equal, so should it not be -Sin? Or can we not do this as it's a function?

And if it's sin to the power of -1, how the hell do I unput that into a calculator?

I just cannot get the last stage of the working out there... Any help would be greatly appreciated!



If it helps, it's a normal Casio scientific calculator I'm using.

[vinnie83]

I also know that 1n2 is the relative refractive index, but is it also a workable equation? And if so, how?

If it was 1n I would know it was 1xn or n2 would be referring to something, but is 1n2 just a way of representing relative refractive index, with no actual mathematical meaning, or is it also a sum of some sort?

Bloody confused if anyone could help... I do regret not paying more attention in A-level maths now

[ndtman]

SHIFT SIN (0.443333156)

[vinnie83]

ndtman said:

SHIFT SIN (0.443333156)

Great, thanks that's cleared that part up!

Any idea as to why it's Sin to the power of -1 and not -Sin when moving from one side of the equation to the other?

[twin40s]

sin-1 refers to the inverse sine (arc sin)

normaly "shift" sine on a calculator

Hope this helps

Paul

[ndtman]

vinnie83 said:

Great, thanks that's cleared that part up!

Any idea as to why it's Sin to the power of -1 and not -Sin when moving from one side of the equation to the other?

Just checked the figures in the question and I get the answer to be 34.32661831 degree (it has been a long day though )

http://en.wikipedia.org/wiki/Snell%27s_law may be of use

[vinnie83]

ndtman said:

vinnie83 said:

Great, thanks that's cleared that part up!

Any idea as to why it's Sin to the power of -1 and not -Sin when moving from one side of the equation to the other?

Just checked the figures in the question and I get the answer to be 34.32661831 degree (it has been a long day though )

http://en.wikipedia.org/wiki/Snell%27s_law may be of use

Sorry to be a pain but, could you tell me where you think the above has gone wrong?

I need to learn this backwards by the weekend as the exam is on Monday!

[Gokartmozart]

ndtman said:

Just checked the figures in the question and I get the answer to be 34.32661831 degree (it has been a long day though )

http://en.wikipedia.org/wiki/Snell%27s_law may be of use

You have inverted the values of n2/n1, should be as in the OP's working. 1.5/1.33 you have used 1.33/1.5

also what Twins40 said about -1 for inverse Sine

[vinnie83]

Gokartmozart said:

ndtman said:

Just checked the figures in the question and I get the answer to be 34.32661831 degree (it has been a long day though )

http://en.wikipedia.org/wiki/Snell%27s_law may be of use

You have inverted the values of n2/n1, should be as in the OP's working. 1.5/1.33 you have used 1.33/1.5

also what Twins40 said about -1 for inverse Sine

1n2 = n2/n1 = c1/c2 = Sin angle 1/ Sin angle 2

Looking back at my working I think I have done it correctly?

[ndtman]

Gokartmozart said:

You have inverted the values of n2/n1, should be as in the OP's working. 1.5/1.33 you have used 1.33/1.5

also what Twins40 said about -1 for inverse Sine

Thanks for that. Good luck for the exam OP.

[ndtman]

vinnie83 said:

Looking back at my working I think I have done it correctly?

You are right. mistake on my part..long day.

Anyhow putting your figures (as near as my mouse skills will allow) results in the following



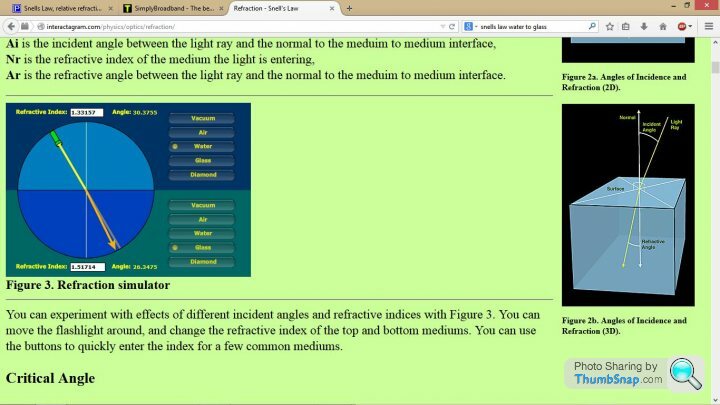
http://interactagram.com/physics/optics/refraction...

[EliseNick]

It looks like your difficulty here has been cleared up. sin^-1 is slightly confusing notation at first, but it is simply the inverse function of sin.

You may find it helpful to stay in symbols for as long as possible, and only put the value in at the end, once you have rearranged the equations into the form you need. This reduces the chance of a numerical error, and gives you a useful general expression. Here, n2/n1 = sin(i)/sin(r) would become r = sin^-1(sin(i)*(n1/n2)) - then plug in the numbers.

Nick

[Martin4x4]

My Google foo is stronger than my memory

This agrees with your answer, 26.3

http://scienceprimer.com/snells-law-refraction-cal...

[Halmyre]

I don't know if it's any help, but useful to remember that for a ray travelling from one medium into another, the refractive index times the sine of the angle is always constant, i.e.

n1*sin(angle1) = n2*sin(angle2); and so on...

(so in your example

1.33*sin(30) = 1.5*sin(angle2)

=> sin(angle2) = (1.33*0.5)/1.5

=> angle2 = inverse of sin(0.443) = 26.3 degrees)

[vinnie83]

Thanks for the help guys it did help, I've managed to get my head around it now