Maths question - Moonwalkers

[budfox]

Twelve men walked on the moon. None were born in February, April, May, or December.

What are the odds that from a randomly selected group of twelve people, there are four months which none of them were born in?

[tapkaJohnD]

A lot lower than you think.

Compare with the "Birthday problem". How many people do you need in a group to have at least two with the same birthday (day and month, not year)? Obviously 367 for certainty, but for 50% probability only TWENTY THREE!

See: http://en.wikipedia.org/wiki/Birthday_problem

JOhn

[Simpo Two]

It would be more remarkable if they had each been born in different months - for example, once Jan-Nov are taken the odds of Astronaut #12 being born in December are 1:12.

Just because one astronaut is born in a particular month does not mean the others are less likely to be.

[budfox]

Yes, I knew about the birthday thing, just wondered what the odds were of the above.

[V8LM]

If four months out of the 12 are free from birthdays, the odds are high:

For the first 8 people they each can be born in a different month so the odds here are 1/1.
For the ninth, they have to share a birthday month with at least one of the other eight. This is 8/12 = 2/3.
For the tenth, they too have to share a birthday month with at least one of the others - 2/3
Same for 11th and 12th. So the final odds are (2/3)^4 which is approx 1 in 5.

The odds that exactly four months are free from birthdays is slightly different.

[RealSquirrels]

0.77 %

edit: I think this is for a given 8 months.

Edited by RealSquirrels on Tuesday 6th May 16:44

[bashful]

This makes me think about the school-year effect, where the oldest kids in each year are most successful (large pinch of salt available on request.) Bearing in mind you would have to be the alpha-est of the alpha males to be an astronaut, I wonder if they got an early start?

[V8LM]

Just to prove myself wrong I resorted to a simple Monte Carlo analysis. I am wrong. The probability of 12 people not having a birthday in any 4 months of the year is 36%; the most likely. Out of 10^11 trials (random number forgiving):

Free months - Percentage probability

0 - 0.0
1 - 0.4
2 - 4.6
3 - 19.9
4 - 35.6
5 - 28.1
6 - 9.9
7 - 1.5
8 - 0.1
9 - 0.0
10 - 0.0
11 - 0.0

So the probability of having at least 4 months in the year where non of the twelve has a birthday is approaching 75%!

(The reason my 1 in 5 above is wrong is that it is based upon the first 8 all having different birth-months. This is unlikely. I am not sure of an easy way to formulate the answer.)

Edited by V8LM on Wednesday 7th May 06:54

[Simpo Two]

V8LM said:

9 - 0.0
10 - 0.0
11 - 0.0

Three months have a probability of zero...?

[V8LM]

Simpo Two said:

Three months have a probability of zero...?

Not zero, but very small. For example, the probability of all twelve having the same birth month is (1/12)^11 = 1.3x10^-12. The probability of all twelve having different birth months is 5.3x10^-5.

[Halmyre]

Here's a thing - is the US population, as a whole, randomly distributed across the 12 months, or is the astronauts' distribution the way it is because the population is skewed anyway?

[V8LM]

Halmyre said:

Here's a thing - is the US population, as a whole, randomly distributed across the 12 months, or is the astronauts' distribution the way it is because the population is skewed anyway?

Having four non-birth months amongst a sample of twelve people is what is expected for an evenly distributed population. However, it does not mean the population is evenly distributed.

[Simpo Two]

budfox said:

Twelve men walked on the moon. None were born in February, April, May, or December.

What are the odds that from a randomly selected group of twelve people, there are four months which none of them were born in?

My own little experiment got almost the same results, with three months unclaimed.

[Halmyre]

V8LM said:

Halmyre said:

Here's a thing - is the US population, as a whole, randomly distributed across the 12 months, or is the astronauts' distribution the way it is because the population is skewed anyway?

Having four non-birth months amongst a sample of twelve people is what is expected for an evenly distributed population. However, it does not mean the population is evenly distributed.

That's what I'm getting at. It's possible there are some months where births are more likely.

Births in April and May correspond with conception in the summer months of July and August. Births in December correspond with conception in March (in spring a young man's fancy, etc.). Births in February correspond with conception in May, which kind of derails my train of thought, unless there's a lot of US public holidays in May.

[V8LM]

Halmyre said:

That's what I'm getting at. It's possible there are some months where births are more likely.

Births in April and May correspond with conception in the summer months of July and August. Births in December correspond with conception in March (in spring a young man's fancy, etc.). Births in February correspond with conception in May, which kind of derails my train of thought, unless there's a lot of US public holidays in May.

http://en.wikipedia.org/wiki/Relative_age_effect


What is interesting, and I'm typing this out again as the network crashed, is looking at the birthdays of all the Mercury, Gemini and Apollo astronauts:

Alan Shepard - November
Gus Grissom - APRIL
John Glenn - July
Scott Carpenter - MAY
Wally Schirra - March
Gordon Cooper - March
Deke Slayton - March

Neil Armstrong - August
Frank Borman - March
Pete Conrad - June
Jim Lovell - March
James McDivitt - June
Thomas P. Stafford - September
Edward Higgins White - November
John Young - September
Buzz Aldrin - January
Eugene Cernan - March
Michael Collins - October
Richard F. Gordon - October
David Scott - June

Roger B. Chaffee - FEBRUARY
Donn F. Eisele - June
Walter Cunningham - March
Rusty Schweickart - October
William Anders - October
Alan Bean - March
Ken Mattingly - March
Jack Swigert - August
Fred Haise - November
Stuart Roosa - August
Edgar Mitchell - September
Alfred Worden - FEBRUARY
James Irwin - March
Charles Duke - October
Ronald Evans - November
Clifton Williams - September
Edward Givens - January
Joe Engle - August

Of the 38 men, ten were born in March, which is three times the 'expected' value. The probability of this happening from a evenly distributed population is less than 0.0007 (I think).

ETA: These data are shown below in graphical form.






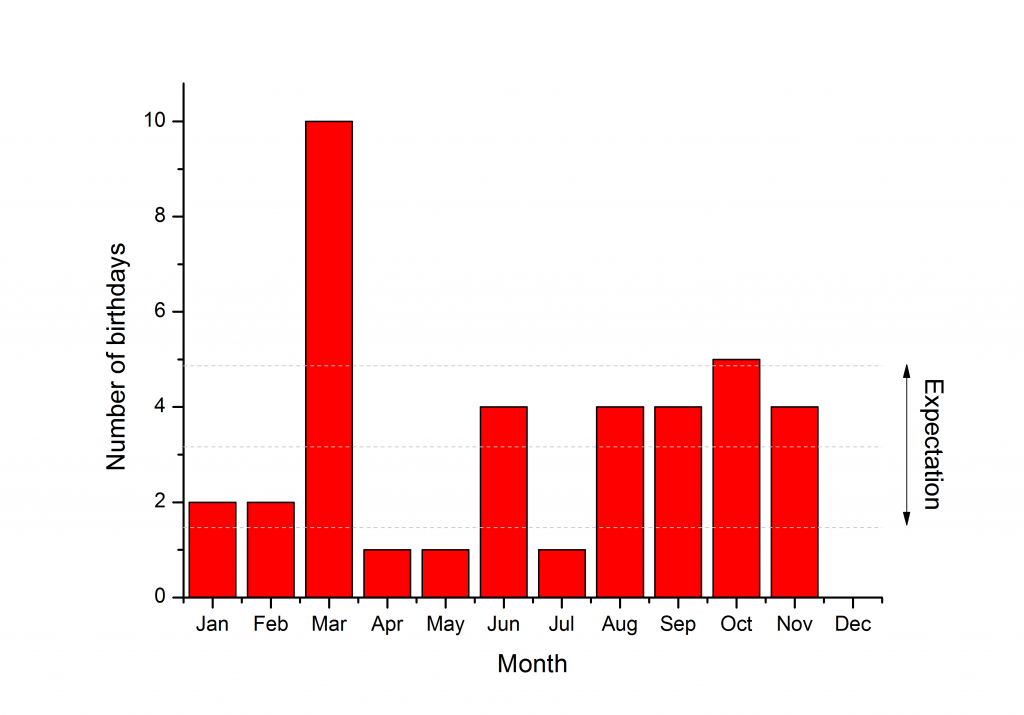
ETA: And Frank Borman and Eugene Cernan share their birthday of March 14th.

Edited by V8LM on Wednesday 7th May 16:34

[nammynake]

38 is a very small sample from which to draw any useful conclusions I guess. The excess in March may be statistically significant using formal statistical tests (chi square) but I wouldn't be convinced that the March excess is genuinely showing a real effect. What would the hypothesis be?

[V8LM]

nammynake said:

38 is a very small sample from which to draw any useful conclusions I guess. The excess in March may be statistically significant using formal statistical tests (chi square) but I wouldn't be convinced that the March excess is genuinely showing a real effect. What would the hypothesis be?

True. Lies. Damn lies. And statistics.

The probability that life evolved from stuff is astronomically small, but it has. A retrospective analysis means little.

I'm just bitter as I was born in December.

[Simpo Two]

V8LM said:

The probability that life evolved from stuff is astronomically small

You don't know that...

As hinted at above, sample size and correct analysis of deviation is essential before you can draw any conclusions.

[Alfanatic]

Results from large sample sizes are more trustworthy than results from small ones.
Results from small sample sizes are likely to be more extreme than results from large sample sizes.

A random distribution is more likely to form clumps than uniformity, and the two statements above predict that the smaller the sample size you select, the more extreme the clumps will appear.

Human nature is to look for patterns and formulate reasons for the patterns. If a sample size is too small then it looks like a pattern and we will search for design or reason behind a pattern which in fact can be nothing more than a predictable accident of sampling.

[Dr Jekyll]

V8LM said:

(The reason my 1 in 5 above is wrong is that it is based upon the first 8 all having different birth-months. This is unlikely.

I got 1 in 5 the same way as you. The way I see it 8 of them must have had different birth months and the sequence of astronauts and birth months is irrelevant. So you can arbitrarily define 8 with different birth months as the 'first' eight. Then work out the chances of the next 4 each avoiding the unused months.