Electrical Capacitance Question
Discussion
Opara said:
Hi, i'm having a problem with this question, it seems like i'm missing something and could do with a jumping off point to get started.If you don't mind could you take a look?
Cheers
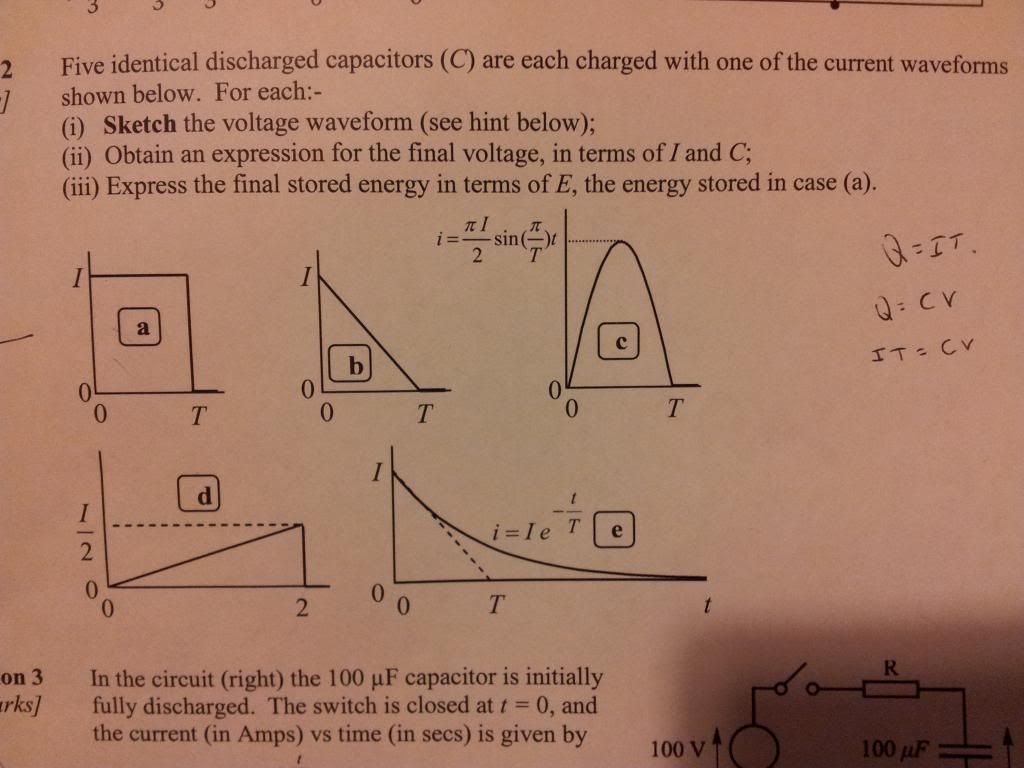
For a capacitor:Cheers
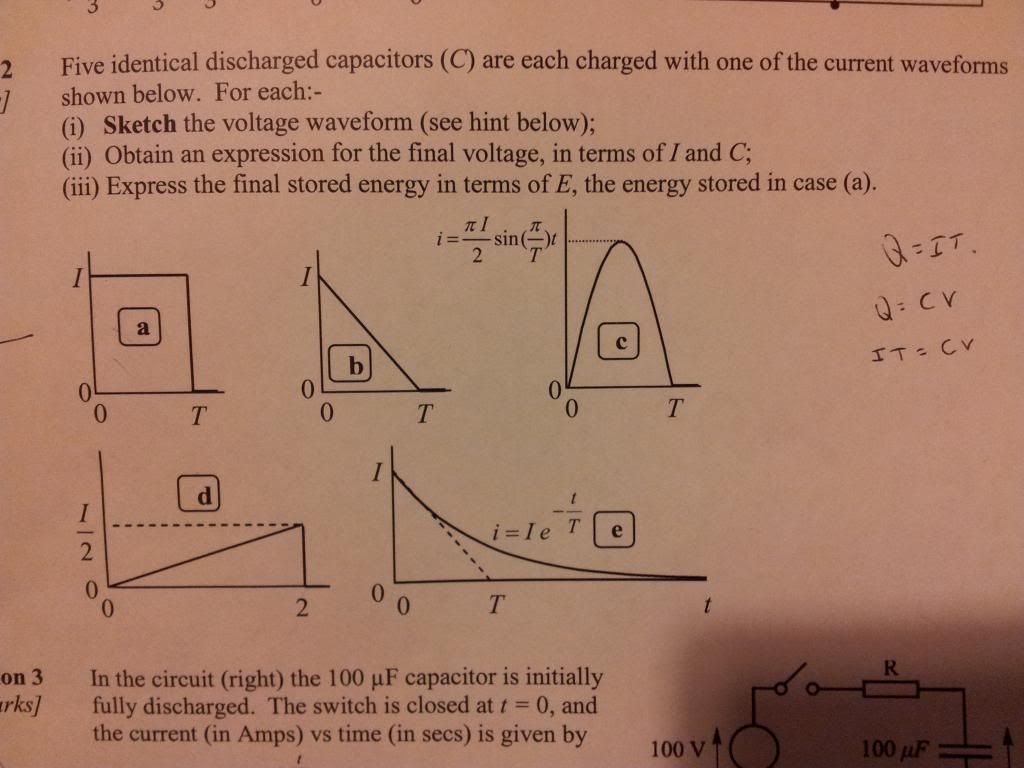
I = C.dv/dt
The current is the given by the rate of change of the voltage. Or if you know the current, then a bit of integration will give the voltage profile.
V = 1/c . integral(I)
You have a graph of I vs t, the integral of I w.r.t t is the area underneath.
Hi, can you tell me if I am on the right lines?
We are only concerned between 0 and T, so for A we look at the graph and see that between 0-T that T=I and so integrating with respect to T would just be iT between the limits of 0-T?
The part that is throwing me is having no numbers to work with.
Thanks
We are only concerned between 0 and T, so for A we look at the graph and see that between 0-T that T=I and so integrating with respect to T would just be iT between the limits of 0-T?
The part that is throwing me is having no numbers to work with.
Thanks
Opara said:
Hi, can you tell me if I am on the right lines?
We are only concerned between 0 and T, so for A we look at the graph and see that between 0-T that T=I and so integrating with respect to T would just be iT between the limits of 0-T?
The part that is throwing me is having no numbers to work with.
Thanks
Correct, but I don't think the question is limited to times between 0 and T. In (a) the current drops to zero at time T so the voltage across the capacitor remains constant for times > T. The graph for (a) is a line from 0,0 to IT/C at time = T and then remains constant at this value for times > T.We are only concerned between 0 and T, so for A we look at the graph and see that between 0-T that T=I and so integrating with respect to T would just be iT between the limits of 0-T?
The part that is throwing me is having no numbers to work with.
Thanks
V8LM said:
Opara said:
Hi, can you tell me if I am on the right lines?
We are only concerned between 0 and T, so for A we look at the graph and see that between 0-T that T=I and so integrating with respect to T would just be iT between the limits of 0-T?
The part that is throwing me is having no numbers to work with.
Thanks
Correct, but I don't think the question is limited to times between 0 and T. In (a) the current drops to zero at time T so the voltage across the capacitor remains constant for times > T. The graph for (a) is a line from 0,0 to IT/C at time = T and then remains constant at this value for times > T.We are only concerned between 0 and T, so for A we look at the graph and see that between 0-T that T=I and so integrating with respect to T would just be iT between the limits of 0-T?
The part that is throwing me is having no numbers to work with.
Thanks
For B, the current is a graph i= -(I/T)t + I. I and T are constants. i is instantaneous current, t is instantaneous time, v is instantaneous voltage.
a) v = (integral)(i/C).dt
=> v= -(I/CT).(1/2)t^2 + (I/C).t + X
between 0 and T. above T, I=0 therefore the voltage is constant at value it was at t=T.
at t=0, v=0(discharged to start), so X=0.
b) Voltage at time T, V = -(I/2CT).T^2 + (I/C).T = (I/2C).T
c) E = (1/2).C.V^2 , where V is the value in b).
Gassing Station | Science! | Top of Page | What's New | My Stuff